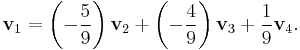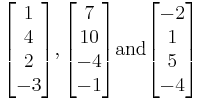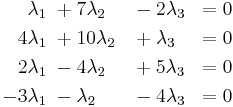Linear independence

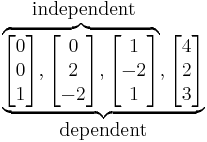
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent. For instance, in the three-dimensional real vector space 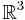$\mathbb{R}^3$ we have the following example.

$\begin{matrix} \mbox{independent}\qquad\\ \underbrace{ \overbrace{ \begin{bmatrix}0\\0\\1\end{bmatrix}, \begin{bmatrix}0\\2\\-2\end{bmatrix}, \begin{bmatrix}1\\-2\\1\end{bmatrix} }, \begin{bmatrix}4\\2\\3\end{bmatrix} }\\ \mbox{dependent}\\ \end{matrix}$

Here the first three vectors are linearly independent; but the fourth vector equals 9 times the first plus 5 times the second plus 4 times the third, so the four vectors together are linearly dependent. Linear dependence is a property of the family, not of any particular vector; for example in this case we could just as well write the first vector as a linear combination of the last three.

$\bold{v}_1 = \left(-\frac{5}{9}\right) \bold{v}_2 %2B \left(-\frac{4}{9}\right) \bold{v}_3 %2B \frac{1}{9} \bold{v}_4 .$

In probability theory and statistics there is an unrelated measure of linear dependence between random variables.

1 Definition
2 Geometric meaning
3 Example I
- 3.1 Proof
- 3.2 Alternative method using determinants
4 Example II
- 4.1 Proof
5 Example III
- 5.1 Proof
6 Example IV
- 6.1 Proof
7 Projective space of linear dependences
8 Linear dependence between random variables
9 See also
10 External links

Definition

A finite subset of n vectors, v₁, v₂, ..., v_n, from the vector space V, is linearly dependent if and only if there exists a set of n scalars, a₁, a₂, ..., a_n, not all zero, such that

$a_1 \mathbf{v}_1 %2B a_2 \mathbf{v}_2 %2B \cdots %2B a_n \mathbf{v}_n = \mathbf{0}.$

Note that the zero on the right is the zero vector, not the number zero.

If such scalars do not exist, then the vectors are said to be linearly independent.

Alternatively, linear independence can be directly defined as follows: a set of vectors is linearly independent if and only if the only representations of the zero vector as linear combinations of its elements are trivial solution solutions i.e. whenever a₁, a₂, ..., a_n are scalars such that

$a_1 \mathbf{v}_1 %2B a_2 \mathbf{v}_2 %2B \cdots %2B a_n \mathbf{v}_n = \mathbf{0},$

if and only if a_i = 0 for i = 1, 2, ..., n.

A set of vectors is then said to be linearly dependent if it is not linearly independent.

More generally, let V be a vector space over a field K, and let {v_i | i∈I} be a family of elements of V. The family is linearly dependent over K if there exists a family {a_j | j∈J} of elements of K, not all zero, such that

$\sum_{j \in J} a_j \mathbf{v}_j = \mathbf{0} \,$

where the index set J is a nonempty, finite subset of I.

A set X of elements of V is linearly independent if the corresponding family {x}_x∈X is linearly independent.

Equivalently, a family is dependent if a member is in the linear span of the rest of the family, i.e., a member is a linear combination of the rest of the family.

A set of vectors which is linearly independent and spans some vector space, forms a basis for that vector space. For example, the vector space of all polynomials in x over the reals has for a basis the (infinite) subset {1, x, x², ...}.

Geometric meaning

A geographic example may help to clarify the concept of linear independence. A person describing the location of a certain place might say, "It is 5 miles north and 6 miles east of here." This is sufficient information to describe the location, because the geographic coordinate system may be considered as a 2-dimensional vector space (ignoring altitude). The person might add, "The place is 7.81 miles northeast of here." Although this last statement is true, it is not necessary.

In this example the "5 miles north" vector and the "6 miles east" vector are linearly independent. That is to say, the north vector cannot be described in terms of the east vector, and vice versa. The third "7.81 miles northeast" vector is a linear combination of the other two vectors, and it makes the set of vectors linearly dependent, that is, one of the three vectors is unnecessary.

Also note that if altitude is not ignored, it becomes necessary to add a third vector to the linearly independent set. In general, n linearly independent vectors are required to describe any location in n-dimensional space.

Example I

The vectors (1, 1) and (−3, 2) in 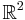$\mathbb{R}^2$ are linearly independent.

Proof

Let λ₁ and λ₂ be two real numbers such that

$(1, 1) \lambda_1 %2B (-3, 2) \lambda_2 = (0, 0) . \,\!$

Taking each coordinate alone, this means

$\begin{align} \lambda_1 - 3 \lambda_2 &{}= 0 , \\ \lambda_1 %2B 2 \lambda_2 &{}= 0 . \end{align}$

Solving for λ₁ and λ₂, we find that λ₁ = 0 and λ₂ = 0.

Alternative method using determinants

An alternative method uses the fact that n vectors in 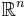$\mathbb{R}^n$ are linearly dependent if and only if the determinant of the matrix formed by taking the vectors as its columns is zero.

In this case, the matrix formed by the vectors is

$A = \begin{bmatrix}1&-3\\1&2\end{bmatrix} . \,\!$

We may write a linear combination of the columns as

$A \Lambda = \begin{bmatrix}1&-3\\1&2\end{bmatrix} \begin{bmatrix}\lambda_1 \\ \lambda_2 \end{bmatrix} . \,\!$

We are interested in whether AΛ = 0 for some nonzero vector Λ. This depends on the determinant of A, which is

$\det A = 1\cdot2 - 1\cdot(-3) = 5 \ne 0 . \,\!$

Since the determinant is non-zero, the vectors (1, 1) and (−3, 2) are linearly independent.

Otherwise, suppose we have m vectors of n coordinates, with m < n. Then A is an n×m matrix and Λ is a column vector with m entries, and we are again interested in AΛ = 0. As we saw previously, this is equivalent to a list of n equations. Consider the first m rows of A, the first m equations; any solution of the full list of equations must also be true of the reduced list. In fact, if 〈i₁,...,i_m〉 is any list of m rows, then the equation must be true for those rows.

$A_{{\lang i_1,\dots,i_m} \rang} \Lambda = \bold{0} . \,\!$

Furthermore, the reverse is true. That is, we can test whether the m vectors are linearly dependent by testing whether

$\det A_{{\lang i_1,\dots,i_m} \rang} = 0 \,\!$

for all possible lists of m rows. (In case m = n, this requires only one determinant, as above. If m > n, then it is a theorem that the vectors must be linearly dependent.) This fact is valuable for theory; in practical calculations more efficient methods are available.

Example II

Let V = Rⁿ and consider the following elements in V:

$\begin{matrix} \mathbf{e}_1 & = & (1,0,0,\ldots,0) \\ \mathbf{e}_2 & = & (0,1,0,\ldots,0) \\ & \vdots \\ \mathbf{e}_n & = & (0,0,0,\ldots,1).\end{matrix}$

Then e₁, e₂, ..., e_n are linearly independent.

Proof

Suppose that a₁, a₂, ..., a_n are elements of R such that

$a_1 \mathbf{e}_1 %2B a_2 \mathbf{e}_2 %2B \cdots %2B a_n \mathbf{e}_n = 0 . \,\!$

Since

$a_1 \mathbf{e}_1 %2B a_2 \mathbf{e}_2 %2B \cdots %2B a_n \mathbf{e}_n = (a_1 ,a_2 ,\ldots, a_n) , \,\!$

then a_i = 0 for all i in {1, ..., n}.

Example III

Let V be the vector space of all functions of a real variable t. Then the functions e^t and e^2t in V are linearly independent.

Proof

Suppose a and b are two real numbers such that

ae^t + be^2t = 0

for all values of t. We need to show that a = 0 and b = 0. In order to do this, we divide through by e^t (which is never zero) and subtract to obtain

be^t = −a.

In other words, the function be^t must be independent of t, which only occurs when b = 0. It follows that a is also zero.

Example IV

The following vectors in R⁴ are linearly dependent.

$\begin{matrix} \\ \begin{bmatrix}1\\4\\2\\-3\end{bmatrix}, \begin{bmatrix}7\\10\\-4\\-1\end{bmatrix} \mathrm{and} \begin{bmatrix}-2\\1\\5\\-4\end{bmatrix} \\ \\ \end{matrix}$

Proof

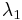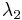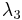We need to find scalars $\lambda_1$ , $\lambda_2$ and $\lambda_3$ such that

$\begin{matrix} \\ \lambda_1 \begin{bmatrix}1\\4\\2\\-3\end{bmatrix}%2B \lambda_2 \begin{bmatrix}7\\10\\-4\\-1\end{bmatrix}%2B \lambda_3 \begin{bmatrix}-2\\1\\5\\-4\end{bmatrix}= \begin{bmatrix}0\\0\\0\\0\end{bmatrix}. \end{matrix}$

Forming the simultaneous equations:

$\begin{align} \lambda_1& \;%2B 7\lambda_2& &- 2\lambda_3& = 0\\ 4\lambda_1& \;%2B 10\lambda_2& &%2B \lambda_3& = 0\\ 2\lambda_1& \;- 4\lambda_2& &%2B 5\lambda_3& = 0\\ -3\lambda_1& \;- \lambda_2& &- 4\lambda_3& = 0\\ \end{align}$

we can solve (using, for example, Gaussian elimination) to obtain:

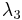$\begin{align} \lambda_1 &= -3 \lambda_3 /2 \\ \lambda_2 &= \lambda_3/2 \\ \end{align}$

where $\lambda_3$ can be chosen arbitrarily.

Since these are nontrivial results, the vectors are linearly dependent.

Projective space of linear dependences

A linear dependence among vectors v₁, ..., v_n is a tuple (a₁, ..., a_n) with n scalar components, not all zero, such that

$a_1 \mathbf{v}_1 %2B \cdots %2B a_n \mathbf{v}_n=0. \,$

If such a linear dependence exists, then the n vectors are linearly dependent. It makes sense to identify two linear dependences if one arises as a non-zero multiple of the other, because in this case the two describe the same linear relationship among the vectors. Under this identification, the set of all linear dependences among v₁, ...., v_n is a projective space.

Linear dependence between random variables

The covariance is sometimes called a measure of "linear dependence" between two random variables. That does not mean the same thing as in the context of linear algebra. When the covariance is normalized, one obtains the correlation matrix. From it, one can obtain the Pearson coefficient, which gives us the goodness of the fit for the best possible linear function describing the relation between the variables. In this sense covariance is a linear gauge of dependence.

External links

Online Notes on Linear Independence.
Linearly Dependent Functions at WolframMathWorld.
Tutorial and interactive program on Linear Independence.
Introduction to Linear Independence at KhanAcademy.

Topics related to linear algebra

Scalar · Vector · Vector space · Vector projection · Linear span · Linear map · Linear projection · Linear independence · Linear combination · Basis · Column space · Row space · Dual space · Orthogonality · Rank · Minor · Kernel · Eigenvalues and eigenvectors · Least squares regressions · Outer product · Inner product space · Dot product · Transpose · Gram–Schmidt process · Matrix decomposition

Linear independence

Contents

Definition

Geometric meaning

Example I

Proof

Alternative method using determinants

Example II

Proof

Example III

Proof

Example IV

Proof

Projective space of linear dependences

Linear dependence between random variables

See also

External links